들어가며..
이 장에서는 신호의 스펙트럼 개념을 소개한다. 이는 신호의 주파수 내용을 간결하게 표현하는 것으로, 사인파들의 합으로 표현할 수 있다. 우리는 2장에서
$$ x(t) = Acos(2\pi f_0t + \phi)$$
$$= Real [Xe^{j 2 \pi f_0 t}]$$
와 같은 사인파의 특성에 대해 배웠다.
위 수식의 x(t)는 진폭 A, 주파수 f0 및 위상 ϕ 세 가지 수로 모든 t에 대해 정의된다. 지난 장에서는 복소 진폭 $$X = Ae^{j \phi}$$을 정의하고 페이저(phasor)라고 부르기로 했다.
위 수식의 신호는 전기 전원망에서 찾을 수 있는 전압 및 전류에 대한 좋은 수학적 모델이다. 전기 회로의 연구에서는 동일한 주파수를 가진 사인파들의 덧셈을 단순화할 수 있기 때문에 페이저를 쓰는 것이 굉장히 유용하다.
하지만 이 장에서는 더 복잡한 파형을 서로 다른 주파수를 가진 정현파들의 합으로 나타낼 수 있는 방법을 제시할 것이다. 명칭은 다중 주파수 신호의 스펙트럼이다. 이는 진폭, 위상, 주파수 정보를 간단하게 정의한 것으로, 이를 통해 신호를 나타낼 수 있다.
그리고 추후에 이 스펙트럼 정보를 그래프로 표현하는 방법도 살펴볼 것이다.
이 스펙트럼 그래프를 이용하면, 서로 다른 주파수의 스펙트럼 구성 요소들 간의 관계를 빠르고 쉽게 파악할 수 있다. 결과적으로, 신호가 어떻게 구성되었는지 이해하는 데 아주 유용한 툴이 될 것이다.
정현파 합의 스펙트럼
정현파가 중요한 이유는 복잡한 신호를 표현하기 위한 기본적인 구성 요소이기 때문이다. 이 장에서는 꽤 복잡해 보이는 파형을 단순한 정현파의 조합으로 구성할 수 있는 방법을 보여줄 것이다.
정현파로부터 새로운 신호를 생성하는 가장 일반적이고 강력한 방법은 가산 선형 결합(additive linear combination)이다. 여기서 실수(Real) 신호는 상수와 N개의 정현파를 각각 다른 주파수, 진폭 및 위상으로 더하여 생성될 수 있다는 것을 의미한다. 즉, 만약 신호가 실수이면, 이는
$$ x(t) = A_0 +\sum_{k=1}^NA_kcos(2\pi f_kt + \phi_k)$$
형태로 표현될 수 있다는 것을 의미한다. 여기서 일반적으로 각 신호의 진폭, 위상, 그리고 주파수가 독립적으로 선택될 수 있다. 이러한 신호는 각각의 정현파 구성 요소에 대한 복소 지수와 복소진폭을 사용하여 표현될 수도 있다. 즉,
$$x(t) = X_0 +\sum_{k=1}^NReal[X_ke^{j2\pi f_kt}]$$
이런 식으로 말이다.
여기서 $$X_0 = A_0$$는 상수를 나타내며, 각 복소진폭 $$X_k = A_ke^{j \phi_k}$$는 회전 페이저의 크기와 위상을 나타내며 그 주파수는 fk로 나타낼 수 있다. 역 오일러 공식을 이용해 위 수식을 다른 형태로 나타내 보자.
$$x(t) = X_0 +\sum_{k=1}^N\left\{\frac{X_k}{2}e^{j 2 \pi f_k t}+\frac{X^*_k}{2}e^{-j 2 \pi f_k t}\right\} (1)$$
이 수식 역시 각 정현파가 두 개의 회전 페이저로 분해된다는 것을 보여준다. 하나는 양의 주파수 fk에서 반시계 방향으로 회전하고, 다른 하나는 음의 주파수 -fk에서 시계 방향으로 회전한다.
(1)의 신호 표현은 2N + 1개의 +- 주파수와 그에 해당하는 2N + 1개의 복소진폭을 사용하여 구성된 정현파로 이루어진 신호를 지정하는 데 사용되므로 이를 쌍방향 스펙트럼(two-sided spectrum)이라고 한다.
구체적으로, 스펙트럼의 정의는 다음과 같다.
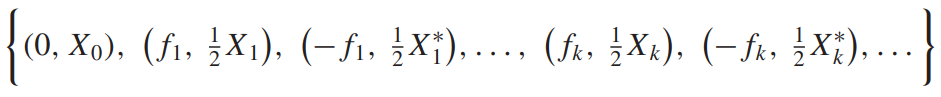
각 $$ (f_k, \frac{1}{2}X_k)$$
는 주파수 라의 복소 지수 성분의 크기와 상대 위상을 나타낸다. 이를 스펙트럼을 신호의 주파수 영역 표현(frequency-domain representation)이라고도 한다.
시간 영역 표현(time-domain representation)은 시간 파형의 값을 제공하는 반면, 주파수 영역 표현은 (1)같이 신호의 정현파 합성 정보를 나타낼 수 있다.
구성 요소의 수가 적고 주파수가 넓게 분포된 경우, 스펙트럼은 신호 x(t)의 간결하고 유용한 표현이 된다. 다음 장에서 더 자세히 살펴보자.
'신호 및 시스템' 카테고리의 다른 글
| 08 (신호 및 시스템)진폭 변조(Amplitude Modulation) (0) | 2024.03.24 |
|---|---|
| 07 (신호 및 시스템)주파수 스펙트럼 그리기 (0) | 2024.03.23 |
| 05 (신호 및 시스템)튜닝포크의 원리와 증명, 물리학 풀이 (1) | 2024.03.20 |
| 04 (신호 및 시스템)역 오일러 공식과 페이저 덧셈법칙, 켤레 복소수 (0) | 2024.03.19 |
| 03 (신호 및 시스템)복소 지수신호의 특성과 페이저 (0) | 2024.03.16 |



