주기신호?
주기 신호는 모든 t에 대해 x(t + T0) = x(t)를 만족하는 조건을 충족하는 신호이다. 이는 신호가 T0초마다 값을 반복한다는 것을 의미한다. 시간 간격 T0는 x(t)의 주기이며, 이것이 가장 작은 반복 간격인 것을 기본 주기라고 한다. 이 섹션에서는 여러 정현파 함수의 합이 주기 신호를 합성하는 데 어떻게 사용되는지를 연구하고, 합산된 정현파 함수가 어떤 주파수 특성을 보이는지 볼 것이다.
주파수는 한 주파수 F0의 정수 배수인 사인 함수의 합으로 신호가 합성 된다.
$$x(t) = a_0 +\sum_{k=1}^N A_kcos(2\pi kF_0 t + \phi_k) .....(1)$$
여기서 주파수라는 아래와 가티 정리할 수 있다.
&& f_k = kF_0&&
여기서 라는 f0의 k번째 하모닉(harmonic)이라고 부른다. 여기서 F0를 기본 주파수(fundamental frequency)라고 부른다.
(1)의 합은 주기적인 신호를 생성하는데, 그러면 x(t)의 주기는 무엇일까? k번째 고조파 사인 함수의 가장 짧은 주기는 1/(kF0)이다. 그러나 이는 또한 1/F0초마다 k번 반복된다.
(1)의 각 코사인은 1/F0의 주기로 반복되므로, 이 합은 정확히 동일한 반복 주기를 가져야 한다. 따라서 x(t + 1/F0) = x(t)이다. 이 주기, T0 = 1/F0,이 가장 짧은 반복 간격인건 쉽게 증명할 수 있으므로, 이것을 기본 주기라고 한다. 다시 말해, 기본 주기는 기본 주파수의 역수이다.
복소 지수 함수를 이용한 표현은 아래와 같다.
$$x(t) = \sum_{k=-N}^N a_ke^{j2\pi kF_0t}$$
여기서 ak는 아래와 같다.
a_k = \begin{cases}A_0 & k = 0\\{\frac{1}{2}A_ke^{j\phi_k}} & k \neq0\end{cases}
합성 모음(Synthetic vowel)
합성 주기 신호중 하나의 예를 들어보자. 이 신호는 기본 주파수가 F0로 100Hz이며 0이 아닌 선분인 {a±2, a±4, a±5, a±16, a±17}. 을 포함하고 있다. 복소 지수 함수의 계수는 아래 표와 같이 나타내겠다. 신호의 스팩트럼도 아래 그림에 명시해 두었다. (a)는 크기에 대한 그래프이고 (b)는 위상에 대한 그래프이다.
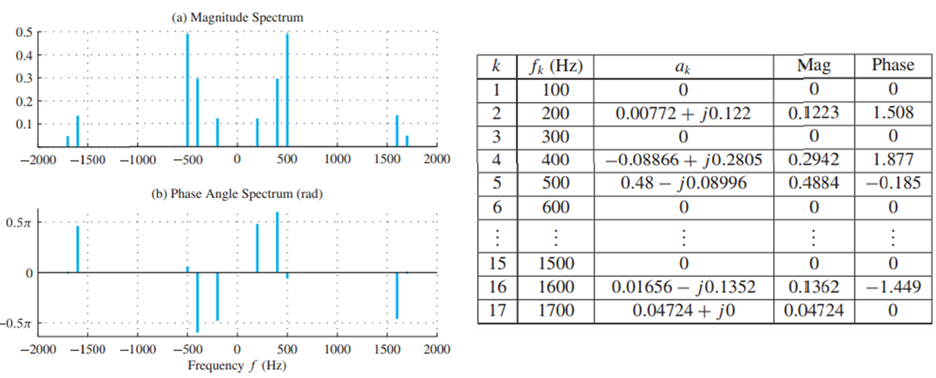
모든 주파수가 100 Hz의 정수배임에도 불구하고, 100 Hz 자체에는 스펙트럼 성분이 없다. 주파수의 최대공약수가 100이므로, 기본 주파수는 100 Hz이고, 기본 주기는 1/100 = 0.01 s이다.
또한 그림 (b)의 음수 주파수 성분은 대응하는 양수 주파수 성분의 위상 각도의 음수이다. 왜냐하면 음수 주파수의 복소 진폭은 해당 양수 주파수의 복소 진폭의 켤레복소수(conjugate)이기 때문이다.
합성된 신호에는 10개의 0이 아닌 스펙트럼 성분이 있지만, 양수와 음수 주파수 항목이 결합된 후에는 다섯 개의 정현파 항목만 남는다. 각 실제 정현파 구성 요소의 기여를 개별적으로 살펴보는 것이 흥미롭다. 우리는 한 번에 하나의 사인파에 해당하는 파형을 연속적으로 그림으로 나타낼 수 있다.
그다음,아래 그림(a)은 위 표의 k = 2 사인파 항목만을 보여준다. 이 단일 구성 요소의 주파수가 2F0 = 200 Hz인데, 이는 파형이 주기적으로 1/200 = 5 ms 주기를 가짐을 의미한다.
다음으로, 아래 그림 (b)는 k = 2 및 k = 4 항목의 합인 x4(t)를 보여준다. 이 두 주파수가 모두 200 Hz의 배수이기 때문에, x4(t)의 주기는 여전히 5 ms이다.
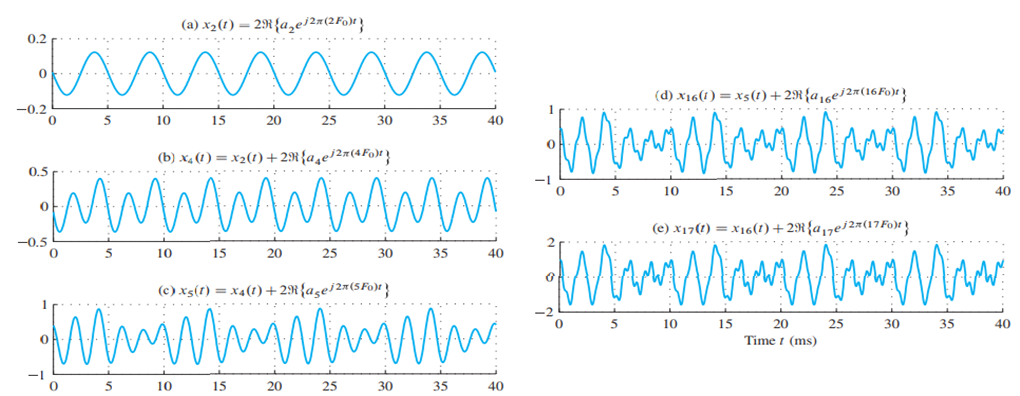
** 그림 설명 : 테이블의 모든 다섯 항목을 합산한 결과. (a) 200 Hz 항목만. (b) 400 Hz와 200 Hz 항목의 합산. 추가 항목이 하나씩 추가되어 (e)에 이르기까지 합성 모음 신호가 생성된다. (c) 기본 주기를 변경하는 500 Hz 항목 추가, (d) 1600 Hz 항목 추가, 그리고 (e) 1700 Hz 항목 추가.
(c)는 처음 세 항목의 합인 x5(t)의 그림을 보여준다. 이제 파형의 주기가 10 ms로 증가한 것을 볼 수 있다. 이는 200, 400 및 500 Hz 세 주파수가 100 Hz의 정수배이기 때문에, 기본 주파수가 이제 100 Hz임을 의미한다. 그림 (d)는 주파수가 1600 Hz인 구성 요소를 추가해도 주기가 변하지 않음을 보여준다. 마지막으로, 그림 (e)는 표의 모든 항목의 합인 x17(t)를 보여준다.
x17(t)의 주기는 F0와 동일한 10 ms인 T0이다. 이는 F0 주파수를 가진 구성 요소가 없더라도 해당된다. 신호 x17(t)는 말소리에서 모음 소리의 파형과 유사하지만, 자연스러운 말소리 신호의 파형을 정확하게 나타내기 위해서는 더 많은 주파수가 필요할 수 있다. 신호의 고주파 성분은 파형의 세부적인 모습에 기여한다. 이는 위 그림에서 확인할 수 있으며, 16번째와 17번째 고조파와 같은 더 높은 주파수 구성 요소가 추가됨에 따라 파형이 점점 복잡해지고 더 빠르게 변한다.